近日，物理科學與工程學院聲子學中心任捷教授團隊在《物理評論快報》（Physical Review Letters）在線發表了題為“Thermodynamic Geometry of Nonequilibrium Fluctuations in Cyclically Driven Transport”的研究論文，給出了受到時間周期性驅動的非平衡輸運過程中的熱力學幾何理論框架。該研究工作從幾何視角出發👩‍🚒，加深了人們對隨機經典/量子熱力學器件的理解，並給出推斷🪫🚶‍♀️‍➡️、控製非絕熱隨機流的一般性思路👨‍🦳。

在近代物理100多年的發展歷程中📓，幾何學提供了一般性的研究思路🈹，包括在愛因斯坦相對論的時空幾何化🫄🏻，量子物理規範場的幾何化，凝聚態物理的幾何拓撲屬性，等一系列經典、量子效應中均發揮了重要作用。作為近代物理學中的核心概念⏸，幾何極大影響了量子力學✅、量子場論♚、凝聚態物理等領域的發展。在量子系統中，量子幾何張量描述了受到驅動的量子系統中態轉移過程的動力學行為。它的反對稱部分對應幾何曲率（Berry曲率），它的對稱部分對應Fubini-Study度規（廣義的黎曼度規）👨‍👩‍👧‍👧。這兩個幾何量在描述孤立量子系統的動力學行為中發揮著核心的作用。

另一方面，開放系統中非平衡熱力學起到的作用引起了人們的極大興趣💛。近些年🏌🏿‍♂️，研究人員試圖使用一個通用的熱力學幾何框架來闡明時間驅動的非平衡輸運中有趣的行為。這涉及周期驅動系統中新穎的輸運行為，涵蓋了隨機量子系統⚈、隨機經典系統🤾🏿‍♂️、宏觀驅動擴散和有限時間過程中的輸運等等。研究表明🛏，時間驅動可以打破熱力學第二定律要求平均熱流自發地從高溫熱庫流向低溫熱庫的限製。除了由瞬時溫差確定的平均動力學熱流外，時間驅動系統中還存在著內稟幾何曲率的貢獻🌂。這種額外的熱流甚至可以產生逆著溫差流動的熱流🤸🏼‍♂️。

任捷教授團隊的最新研究工作指出🦻，在極緩慢驅動導致的絕熱輸運效應之上◽️，還有有限速率驅動導致的非絕熱輸運效應。該非絕熱輸運效應則由時間反轉對稱的幾何度規項描述（如圖1所示），這與時間反對稱的絕熱幾何曲率的貢獻有根本不同。上述的幾何流（包括非絕熱的度規貢獻和絕熱的曲率貢獻）均會對漲落定理和熱力學不確定性關系產生巨大影響。該工作表明🦶🏼，非平衡熱力學幾何可以被用來描述非平衡周期驅動系統的熱力學，並由此推導出一般性的熱力學約束。

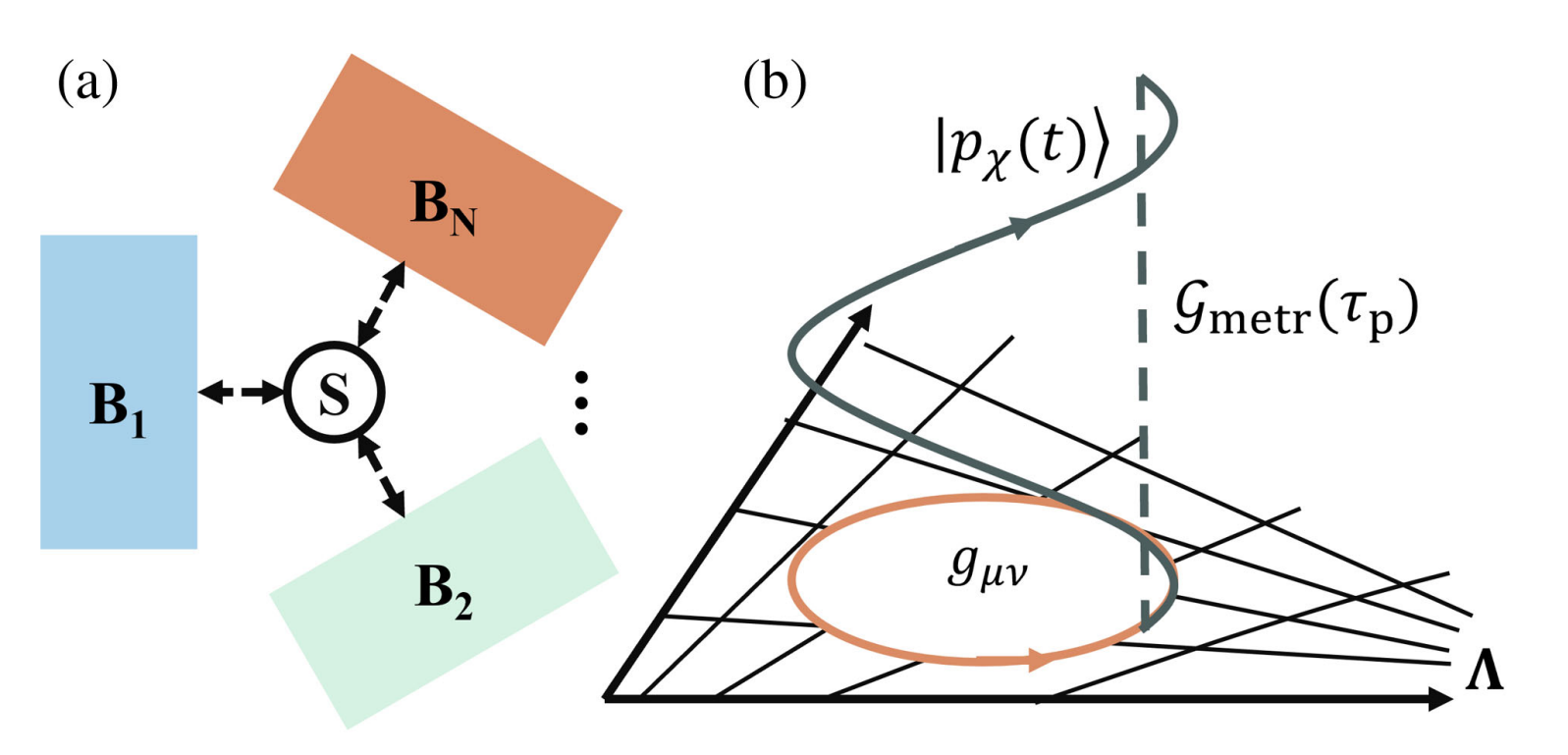
圖1（a）受到周期參數調製的非平衡輸運體系（b）有限時間（非絕熱）驅動帶來的漲落流可以用一個生成函數（虛線）描述，它對應了參數空間中度規量的貢獻

該研究成果進一步討論了非絕熱幾何度規在近絕熱條件下的特殊情況。傳統的熱力學度規僅僅可以描述近平衡條件下的平均熵增🦩，而本研究工作則可以描述任意輸運流的各階漲落效應🤸🏼。它的一個應用是🚴‍♀️，可以給出消除非絕熱泵浦效應（熱絕熱控製）的幾何視角（如圖2所示）🧖🏼‍♀️。該理論框架可以用來進一步研究壓縮✷、相幹性等量子非平衡態存在時🚵🏼‍♀️，有限時間過程中任意隨機流漲落的性質。這是突破傳統熱力學幾何的重要理論進步。

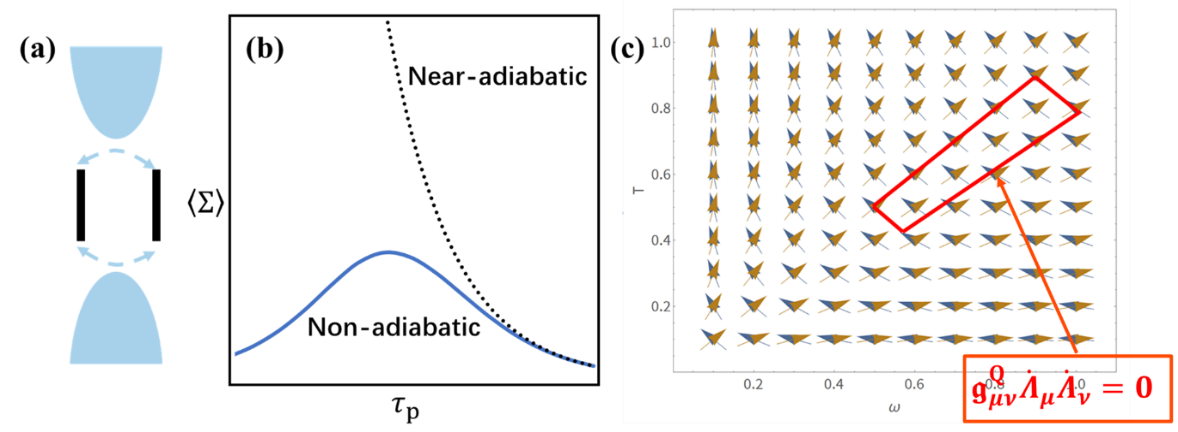
圖2（a）非平衡二能級系統（b）近絕熱的幾何度規流（點線）與任意非絕熱的幾何度規流（實線），在驅動周期較大時兩者重合（c）平均流的度規給出非絕熱控製（消除非絕熱流）的驅動方案，如紅線所示

物理科學與工程學院博士生王子為論文第一作者，任捷教授為論文通訊作者♛。該研究工作受到國家自然科學基金委重點項目、上海市原創探索項目、上海市優秀學術帶頭人以及上海市特殊人工微結構材料與技術重點實驗室等支持🤽🏿‍♀️。

近年來🚵‍♀️👨‍🎤，恒达平台物理科學與工程學院聲子學中心任捷教授團隊在非平衡量子/經典熱輸運和熱力學幾何研究中取得了一系列標誌性成果，在課題組早期關於隨機量子🧑🏼‍🦳🐻、經典非平衡絕熱幾何泵浦的研究基礎上🍈🤸‍♀️，近些年討論了非平衡時空驅動熱擴散中的幾何熱泵與幾何對熱非互易性的限製、熱電幾何泵浦、幾何熱泵浦效應與其中的熱力學不確定性關系💙、有限時間周期驅動輸運中的非平衡熱力學幾何理論、量子熱器件中的圈流拓撲分析等🚟。其中，非平衡輸運中的絕熱幾何相效應與非絕熱度規效應分別受邀發表相關綜述文章🦻🏻。

論文鏈接🦸🏽：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.207101